Take a look at the image on the left. What do you notice? You may recognize this image to be a graph. You may also know that this graph comes from a lesson written by inquiry mathematics advocate Jo Boaler. Boaler’s goal in her lesson, is for students to understand that graphs show comparisons. However, you’ll notice one difference between the image on the left and the image Boaler uses in her lesson plan. In this image, I have taken out the labels on the axis. My reasoning? Because I believed my students could figure that part out themselves.  

I asked the following set of questions to my 4th grade classes.

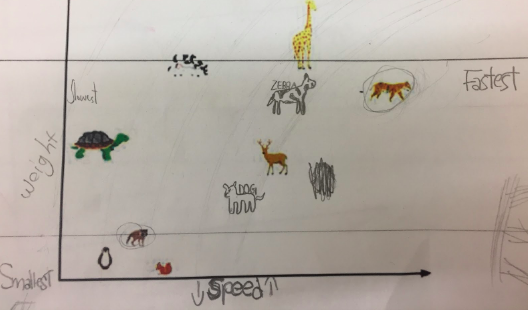
• What can you tell me about this image? 
• What would you label the axises? 
• Where would you place a zebra? What about a dog?

Not only were my students able to correctly label the axises, but they also were able to infer where a dog and where a zebra would be appropriately placed on the graphs. Interestingly, each group had their own perspective as to where a “dog” and where a “zebra” would go providing opportunity for a unique classroom discussion on perspective. There can be different breeds of dogs, so why couldn’t this be placed differently!

Good inquiry mathematics stretches with the ideas of the children in the classroom. We took this one day exercise and turned it into a 3-day math project, as students wanted to create their own graphs similar to Jo Boaler’s animal one. My students researched topics such as flags of countries and weights of planets, and built their own graphs comparing and contrasting areas of interest. While starting off as just a math lesson, this project grew to incorporate geography, science, and social studies into math.

Some examples of my student’s final graphs. They wanted to leave the axis’s off to have other peers and community members guess what they were comparing on their graphs. Can you guess?

For this math lesson, I broke my students into small groups and allowed them time to play with tangrams to explore how the shapes fit together. Once they had about 5 minutes to play, I asked them some guiding questions to begin discovering fractions.

• How many times does the small triangle fit into the larger triangle? 
• How many times does it fit into the small square? 
• If the small triangle fits into the small square 2 times, what fraction of a small square is a small triangle?

Of course these questions were basic for my 4th grade students, but I wanted them to determine that although all the shapes are different sizes, each shape can be measured using the smallest triangle. 

Next, I let my students play again! I gave my students 5 more minutes to play with the pieces but told them that by the end of the 5 minutes they must have some sort of picture created with the blocks. This picture should not have more than 10 pieces, and should include at least 3 different colors of pieces. I showed them this picture of a house as a simple picture I made using my requirements. 

Once each group of students agreed on a picture, I first went around and took a picture of each one. This is mostly because I didn’t want someone to bump the table and the kids to not remember what color piece went where. With the images documented, I had my students pull out their math notebooks to answer the following question: What fraction of your total picture is each color?

Answering was a challenge for many of my students. Even with the guiding questions at the beginning, I had students tell me that in the picture on the right blue is 3/10th of the total because 3 pieces were blue out of 10 total. But with some patience and some partner work, most of my students came to quickly understand this misconception and determine a strategy to accurately answer this journal prompt!

As an introduction to compound shapes I arranged pieces of artwork my students had completed into three different shapes on the board: an L, a snake, and a straight line. The artwork came directly from our unit on imagination, where students drew pictures to fill a nine frame square.The kids loved using their art as the base of math, connecting to the problem because their pieces were being used on the board. 

First, I asked my students: Does each compound shape have the same area? Answers varied and as a class we calculated that each shape does indeed have the same area.

Next, I asked my students: does each compound shape have the same perimeter? Again, answered varied and we calculated as a class that each shape had the same perimeter as well.

For our independent challenge I had students work out an answer to the following question:

Is there a way I can arrange these boxes to have the same area but a different perimeter? 

Students loved this challenge as it provided them with an opportunity to disprove the belief that shapes with the same area must have the same perimeter. They ultimately discovered that if they moved these four nine-frame boxes into a square that the area remained 36 square units, but the perimeter switched from being 30 units to being only 24 units around. 

This was a fun center idea for students to determine Obtuse, Acute, and Right Angles. The kids taped up some old tables outside in the common space to create intersections of different sized angles. Next, in small groups the class took turns labeling each angle with it’s corresponding name based on it’s size.

A few days later, once we introduced angle degrees and measurement using protractors, the kids were again able to use these tables in small groups, this time to measure how big each angle was. The tape provided an extra challenge, as the kids figured out they needed to measure from the inner tape line

Who doesn’t like mixing food with learning? Today we investigated how many M&M’s we thought were in one bag using a scale to weigh in grams. As a whole class, we inquired into how the scale works, playing with it’s functions. Next, I drew popsicle sticks to determine groups of four students to work together to reach a conclusion of how many candies there were. The group got to pick either a crispy bag of m&m’s or a regular bag of m&ms to experiment with. The rules were simple: use any strategy you want to figure out how many m&m’s are in the bag. Yes, you can open the bag and use the m&m’s but no, you cannot count the m&m’s one by one, you must somehow use the scale.

Hint: Look at the back to figure out what the total weight of the package is.

The results for this lesson were varied. Many students got frustrated since when they weighed only one m&m the scale weighed 0kg but when they weighed two m&m’s it sometimes weighed 2kg. Regardless, the students had fun, used teamwork, developed skills on how to use a scale, and were creative in their approaches to get reasonable results whether or not they were totally accurate.

During a weekend trip to Seoul, I went to a pizza shop in Itaewon selling a wide variety of types of pizza. My friend and I debated over whether we would pizza multiple slices or a whole pizza, and ultimately decided that we would go for slices to try more kinds. Good thing we did since each slice was huge, and 3 slices made up half a pizza! This got me thinking . . . mathematically, this wouldn’t make sense for the pizza shop to even sell whole pizzas at all! This is how I got my idea for a lesson I taught the next day at school.

Act I: What do you notice in this picture? What do you wonder about what you are looking at?

Students discussed that this must be a pizza shop and how the numbers represented the prices. They determined that triangles must mean prices for single slices and circles must mean prices for full pizzas.

Act 2: How many slices do you think the pizza shop should sell in their whole pizzas?

We discussed what they remembered from a previous unit on businesses and how businesses normally price items in order to make a profit.

Act 3: This pizza shop sells 6 slices per pizza. How does this compare to your answer? Do you think the pizza shop should change the number of slices per pizza? Why or why not?